一线三等角模型阅读综合题型解析

一线三等角模型阅读题型解析

综合与实践

（1）问题情境

一线三等角是一个常见的相似模型，指的是有三个等角的顶点在同一直线上构成的相似图形，这个角可以是直角，也可以是锐角或钝角。

如图1，∠1=∠2=∠3，由∠2+∠CEA+∠C=∠1+∠CEA+∠DEB=180°可得：∠C=∠DEB，故∠ACE∽∠BED.

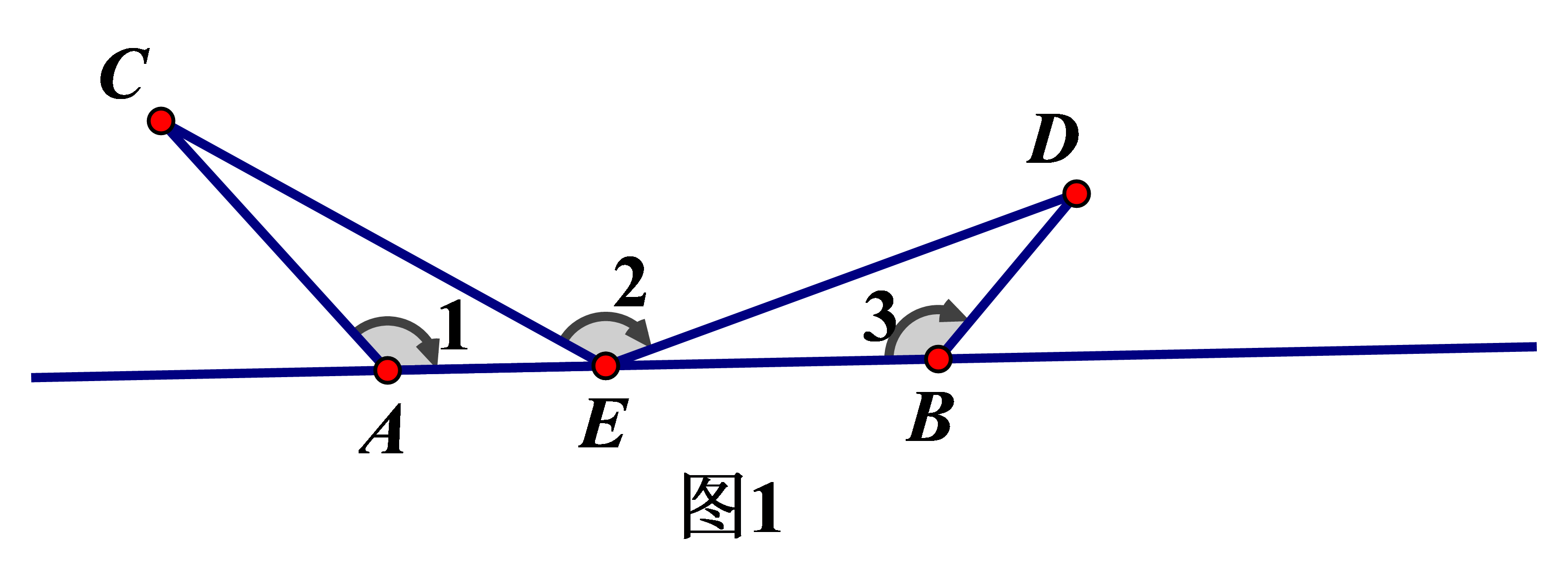
（2）问题解决

①如图2也是一线三等角问题，当∠1=∠2=∠3时，求证：△ACE∽△BED.

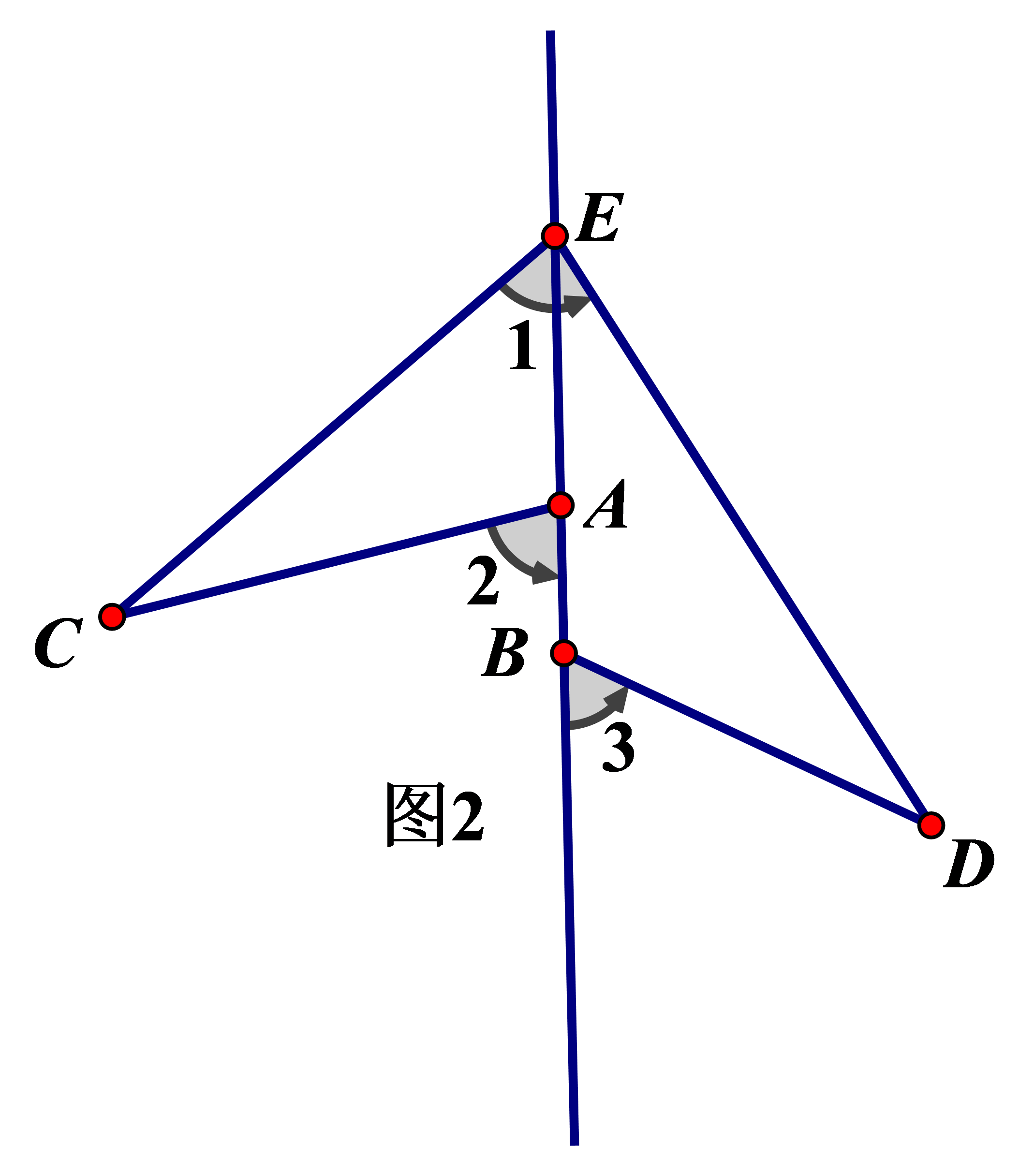
解析：因为∠1=∠2=∠3

由图可得∠2=∠CEA+∠C，∠1=∠CEA+∠DEB（运用外角等于不相邻两内角的和与角的和差得到）

所以∠C=∠DEB

又180°-∠2=180°-∠3

所以∠CAE=∠EBD（等角的外角相等）

所以△ACE∽△BED.

②如图3，等腰直角ABC的直角边AB的长为4，P为斜边BC上一点，且BP=2，D为AC上一点，且∠APD=45°，试求CD的长。

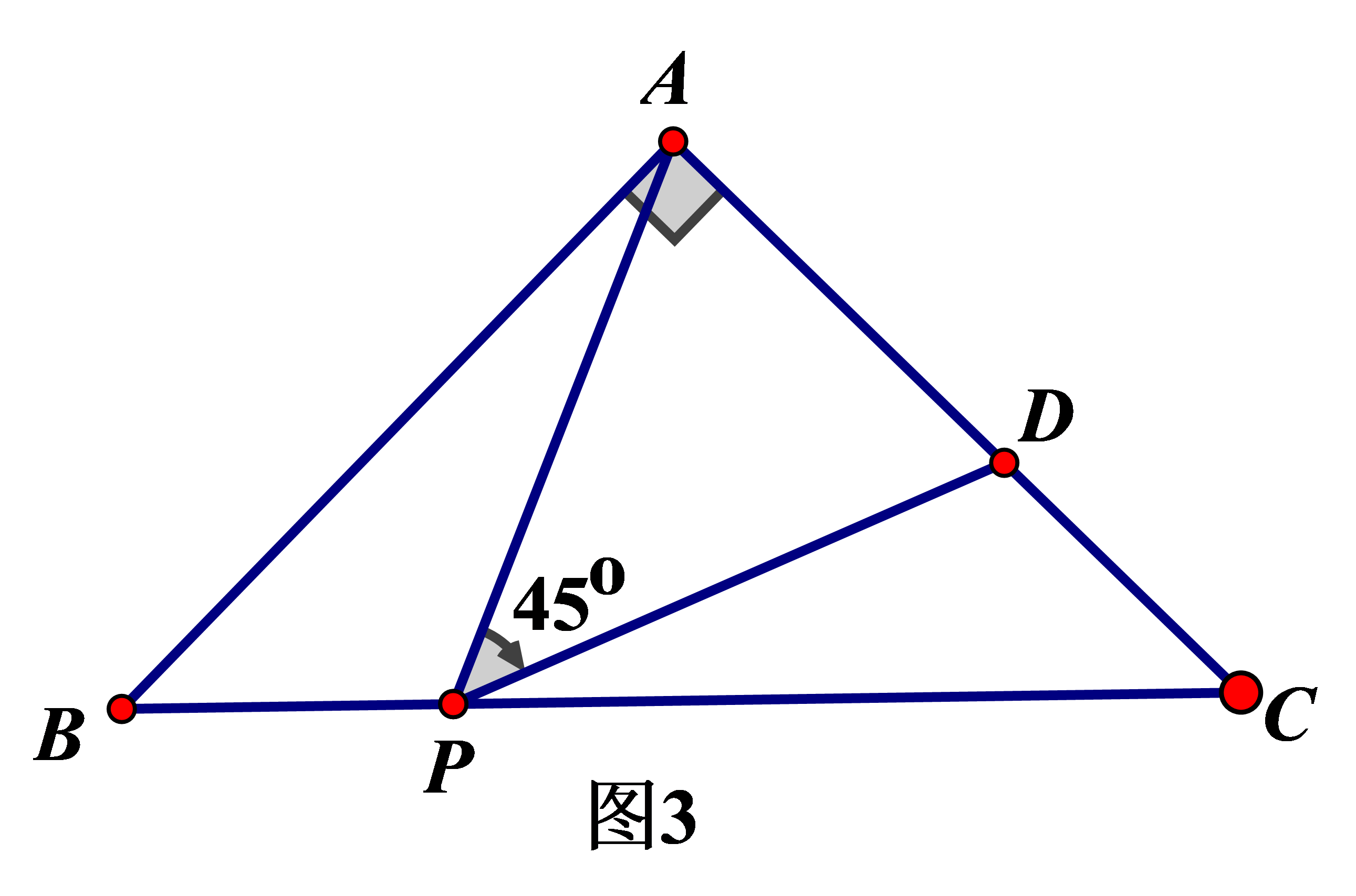
分析：由上面的图1分析可知本题属于一线三等角类型，可证三角形相似。

解：因△ABC是等腰直角三角形，所以∠B=∠C=45°，BC=√2AB=4√2

因为∠B+∠BAP+∠BPA=∠CPD+∠APD+∠BPA=180°，∠APD=45°

∠B=∠CPD

所以△APB∽△PDC

所以CD：BP=PC：AB

即CD：2=（4√2-2）：4

CD=2√2-1

（3）问题拓展

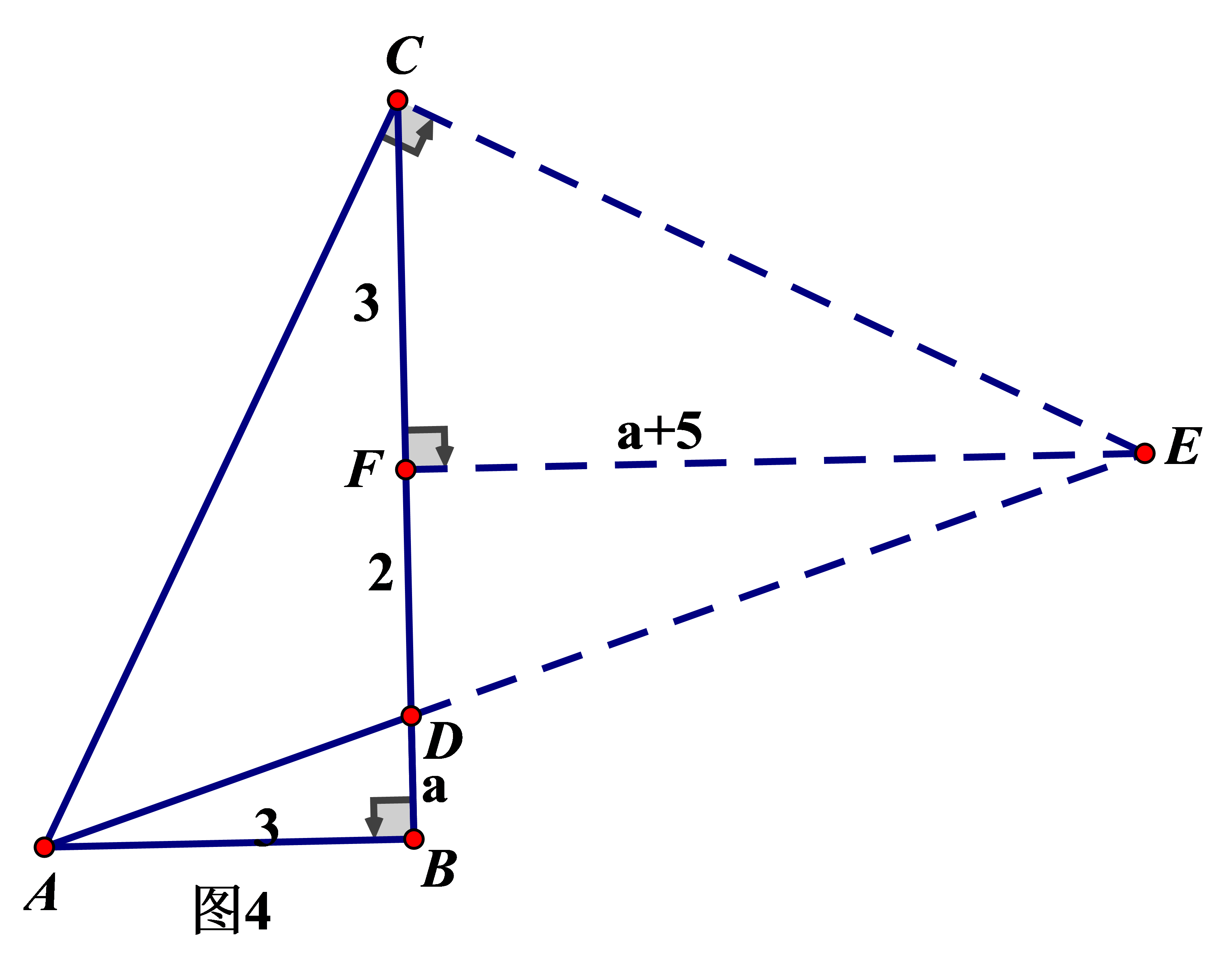
①如图4，ABC中，∠B=90°，∠CAD=45°,AB=3,CD=5，求BD的长；

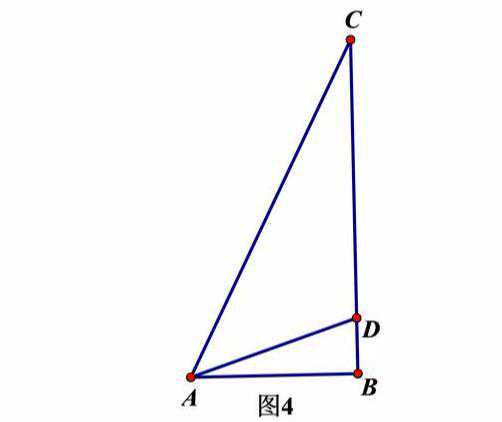
观察问题情境两种结构，构建向图2形状一线三等角类型，（作CE⊥AC交AD的延长线于点E，作EF⊥BC于点F,）如下图，通过同样的思想可证△ABC≌△CDF，从而得EF=a+5,CF=3,于是DF=2,再证△ABD∽△EFD，构建关于a的比例式，a:2=3(a+5)从而可求出a=1或a=-6(舍去)。

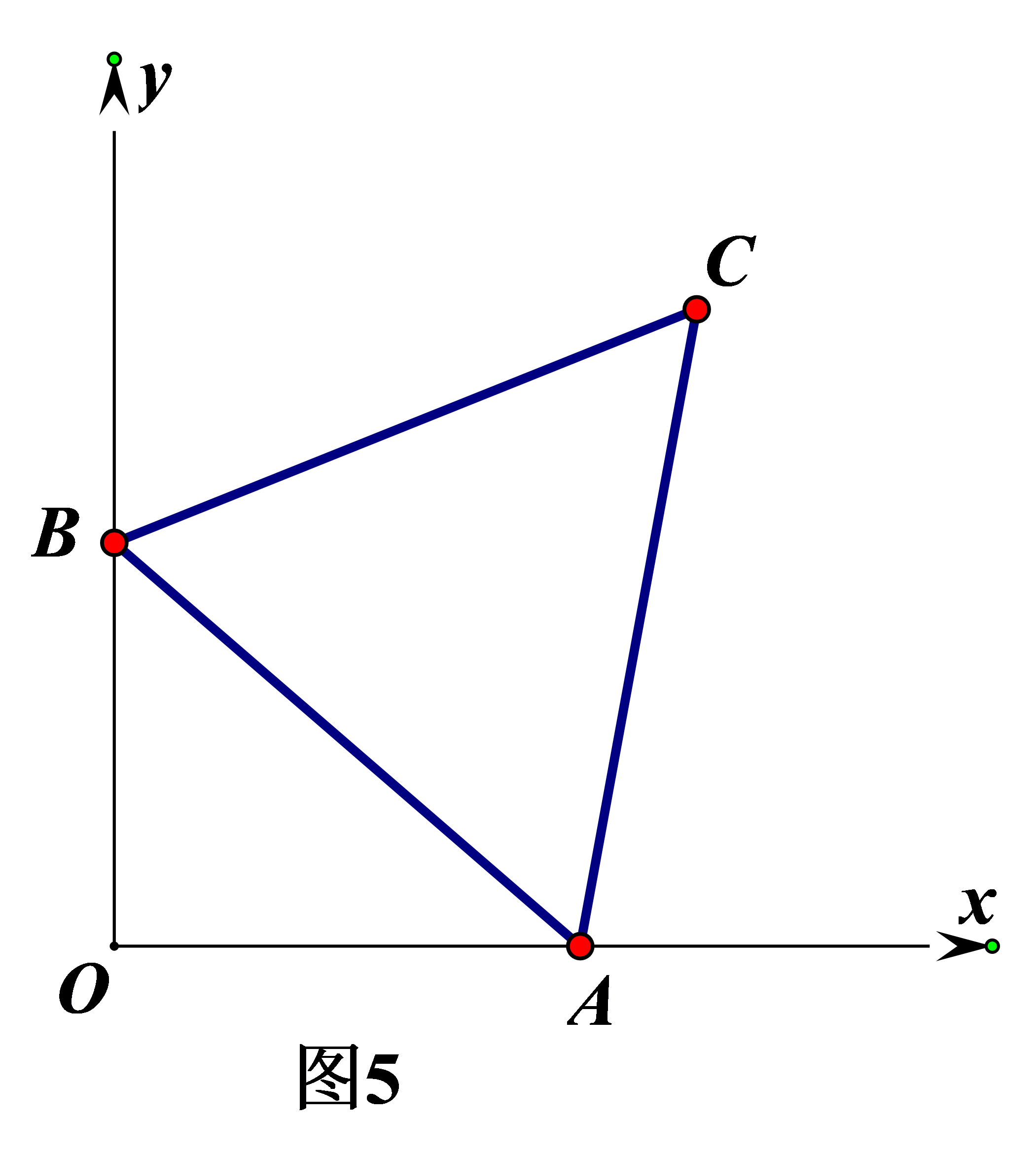
②如图5，在平面直角坐标系中，点A的坐标为（4，0），点B的坐标为（0，2√3）点C在第一象限内，使得ABC是等边三角形，直接写出点C的坐标是________.

解析：做如图辅助线，CD⊥AB，Ef∥x轴，CF⊥EF构建一线三等角模式∠BED=∠BDC=∠DFC=90°，从而可证△BED∽△DCF，

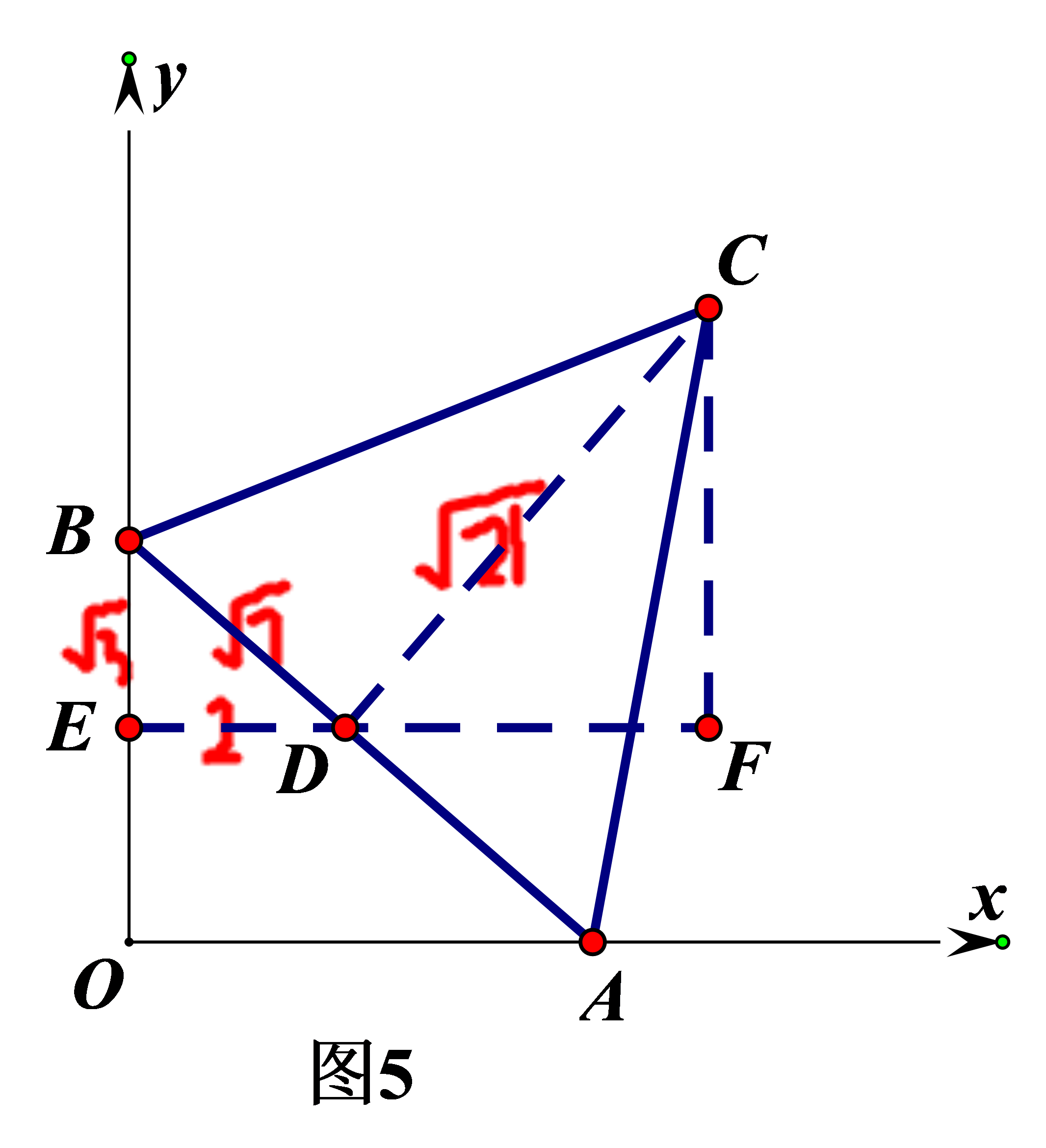
由三线合一，平行线分线段成比例定理，以及勾股定理可得AB=2√7，BD=AD=√7，BE=√3，DE=2，CD=√21，由相似对应边成比例列式可求出DF=3，CF=2√3，所以点C的坐标为（5，3√3）

（解析：铭）